The Role of Internet Development on Energy Intensity in China: Evidence From a Spatial Econometric Analysis

I. Introduction

In this paper, we examine how the development of internet has impacted energy intensity in China. Our hypothesis is that internet development reduces energy intensity. The proposed relationship between internet development and energy intensity is motivated by the theory of information communication technology (ICT) and electricity consumption (EC) proposed by Cho et al. (2007). The ICT-EC theory argues that there is a significant negative relationship between ICT and EC. This theory predicts that internet development will have a positive effect on energy intensity. The hypothesis test we propose is important because China needs to find new ways to solve the dilemma of energy constraints in the era of digital economy (Wu et al., 2019).

To test our proposed hypothesis, we employ Chinese provincial level data covering the 2006-2017 period and find that internet development effectively promotes the decline in energy intensity. These findings make two contributions to the literature. The first is that this paper shows that the development of internet can reduce energy intensity, which further complements the theory of ICT and energy consumption. In fact, there is no literature on how the internet development affects the energy intensity. Our study fills this gap. The second is that the spatial spillover effect of internet development on energy intensity is investigated; this is one aspect of the literature not explored previously.

II. Data and Methodology

A. Methodology

Spatial econometric model

The theoretical framework for this study rests upon the highly popular conceptual framework, namely the Stochastic Impacts by Regression on Population, Affluence, and Technology (STIRPAT) model (Rafiq et al., 2016). The model can be specified as follows:

$$E = \ F\ (P,\ A,\ T,\ Z)\hspace{35mm}(1)$$

Where, E is energy intensity; P represents population; A indicates affluence; T is technological progress; and Z indicates other factors affecting energy intensity, such as science and technology. Based on the theory of ICT and EC proposed by Cho et al. (2007), the STIRPAT model is extended in this paper. In other words, internet development is added to model (1) as part of other variables that affect energy intensity. In addition, according to Hao et al. (2020), energy consumption is spatially dependent; therefore, we use a spatial econometric model to estimate the relationship between internet development and energy consumption. Model (1) is further transformed into the following empirical model:

$$\begin{align*} eci_{it} = \alpha_{0} + \alpha_{1}\textit{internet}_{\text{it}} + \alpha_{2}&\textit{pop}_{\text{it}} + \alpha_{3}\textit{pgdp}_{\text{it}} + \alpha_{4}\textit{rd}_{\text{it}} +\\ &\alpha_{5}W*\textit{internet}_{\text{it}} + \alpha_{i} + \varepsilon_{\text{it}}\hspace{7mm}(2) \end{align*}$$

Where, eci represents energy intensity; $internet_{it}$ is the internet development; $pop_{it}$ represents population; $pgdp_{it}$ indicates affluence; $rd_{it}$ is technological progress; W represents spatial spillover effect; the individual fixed effect is represented by $\alpha_{i}$; and $\varepsilon_{it}$ is the random error term. The spatial Durbin model is used for the regression analysis in this paper.

Spatial weight matrix

In this paper, spatial weight matrix mainly includes the geographic distance weight matrix, $W_{1}$ and the economic weight matrix, $W_{2}$. In addition, in order to avoid possible measurement errors of the distance between the full samples, different thresholds are selected to set the local spatial weight matrix. This follows the study of Hao et al. (2020) and we set the thresholds as 400 kilometers, 600 kilometers, 800 kilometers, 1000 kilometer, 1500 kilometers and 2000 kilometers to investigate the impact of internet development on energy intensity in China.

Spatial autocorrelation test

In this paper, $\text{Moran’s I}$ index is used for spatial autocorrelation test. The calculation method of $\text{Moran’s I}$ index is shown in equation (3):

$$\text{Moran's I=}\sum_{\text{i=1}}^{N}{\sum_{\text{j=1}}^{N}W_{\text{ij}}}\left( x_{i}\text{-}\bar{\text{x}} \right)\left( x_{j}\text{-}\bar{\text{x}} \right)\text{/}\text{S}^{2}\sum_{\text{i=1}}^{N}{\sum_{\text{j=1}}^{N}W_{\text{ij}}}\hspace{10mm}(3)$$

In model (3), the energy intensity of province i is represented as $x_{i}$, and N represents the total number of geographic units (the provinces in this article), $\bar{x}$ represents the average value of energy intensity, and $S^{2}$ represents the variance of the energy intensity level. In addition, $\text{Moran’s I}$ can be statistically tested by the Z value. The specific formula is:

$$Z\left( \text{Moran's I} \right) = \frac{\text{Moran's I-E}\left( \text{Moran's I} \right)}{\sqrt{\text{VAR}\left( \text{Moran's I} \right)}}\hspace{13mm}(4)$$
where $E\left( \text{Moran's I} \right) = - \frac{1}{n - 1}$.

B. Data

According to previous studies, energy intensity is measured by energy consumption per unit of GDP (Chang et al., 2015; Wu et al., 2019). As for the internet development, most scholars use single indicators, such as internet penetration rate and the number of websites, to proxy the internet development level (Czernich et al., 2011; Koutroumpis, 2009). In fact, although the above single indicators are important indicators of the level of internet development, some indicators can only reflect the local facts of internet development and cannot objectively reveal the real level of internet development. Therefore, this paper constructs a measure of internet development level in China from four dimensions of internet popularization: namely, internet infrastructure, internet information resources, and internet application. We use the entropy method to calculate the comprehensive level of internet development in China. The evaluation system of China’s internet development level is shown in Table 1.

In addition, we have several control variables, such as population, GDP per capita, and R&D investment intensity, as proxies for population (pop), wealth (pgdp) and technology (rd), respectively (Hao et al., 2020; Wu et al., 2019). The GDP series has been converted to the constant 2006 price. In this paper, the panel data for 30 Chinese provinces are for the 2006-2017 period. Due to the lack of data, Hong Kong, Macao, Taiwan and Tibet regions with more missing values are excluded. Relevant data are from the China Statistical Yearbook, the China Internet Development Statistical report, the China Science and Technology Statistical Yearbook, and the China Energy Statistical Yearbook^[1].

III. Empirical Results

A. Spatial correlation test

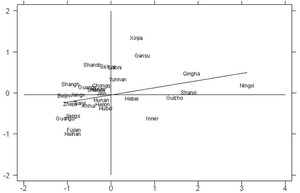
A geographic distance weight matrix, economic weight matrix, and six local spatial weight matrices are used. Based on these eight weight matrices, the $\text{Moran’s I}$ energy intensity in 30 provinces in China for the 2006 to 2017 period is calculated. The significance of the results is tested by using the Z distribution. The specific results are shown in Table 2. Columns 3 to 10 in Table 2 are “Moran’s I” of the local weight matrix based on geographic distance weight matrix, economic weight matrix, and 400km, 600km, 800km, 1000km, 1500km and 2000km thresholds. From Table 2, we see that during the 2006-2017 period, all “Moran’s I” are significant at least at the 10% level of significance. Therefore, China’s energy intensity is characterized by significant spatial dependence. In addition, most of China’s provinces were located in the first and third quadrants in 2006 (see Figures 1), indicating that China’s energy intensity has spatial correlation.

Figure 1:Scatter plot of the Moran index of China’s energy intensity in 2006 (W₁ as spatial weight matrix)

This figure reports results of the Moran index test. Moran index chart can directly show whether there is spatial correlation of China’s energy intensity. The sample in the figure represents different provinces in China.

B. Regression results of spatial econometric model

In the previous section, we found that China’s energy intensity has spatial correlation. This section studies the impact of internet development on energy intensity. According to Table 3, under different types of spatial weight matrix, the coefficient of internet development is significantly negative. This result shows that internet development reduces energy intensity. Meanwhile, under the spatial weight matrix with different distances, the coefficients of internet development show that it rises first then falls as the spatial distance increases. Interestingly, from the perspective of spatial spillover effect (W*internet), internet development has promoted energy intensity of adjacent areas. The spatial spillover effect of internet is not significant only when the spatial weight matrix is 400km. In addition, from the regression results of the control variables, there is no significant correlation between population and energy intensity; the increase in per capita GDP reduces energy intensity; and the progress of science and technology promotes energy intensity, but it is only significant in economic weight matrix, W1000, W1500 and W2000.

IV. Conclusion

This paper studies how the development of the internet affects energy intensity by using the spatial Durbin model and China’s inter-provincial panel data from 2006 to 2017. First, we use the entropy method to measure the level of internet development level in different Chinese provinces from the perspectives of internet popularization, internet infrastructure, internet information resources and internet application. Second, a variety of spatial weight matrices are constructed to test the relationship between internet development and China’s energy intensity. The results show that the development of internet has generated a spatial spillover effect, which significantly reduces the energy intensity, but increases the energy intensity of the adjacent areas.

Acknowledgment

The authors acknowledge financial support from the National Natural Science Foundation of China (71761137001, 71403015, 71521002), the Beijing Natural Science Foundation (9162013), the key research program of the Beijing Social Science Foundation (17JDYJA009), the National Key Research and Development Program of China (2016YFA0602801, 2016YFA0602603), the Joint Development Program of the Beijing Municipal Commission of Education, and the silk road foundation of Xinjiang University (JGSL17021). The usual disclaimer applies.